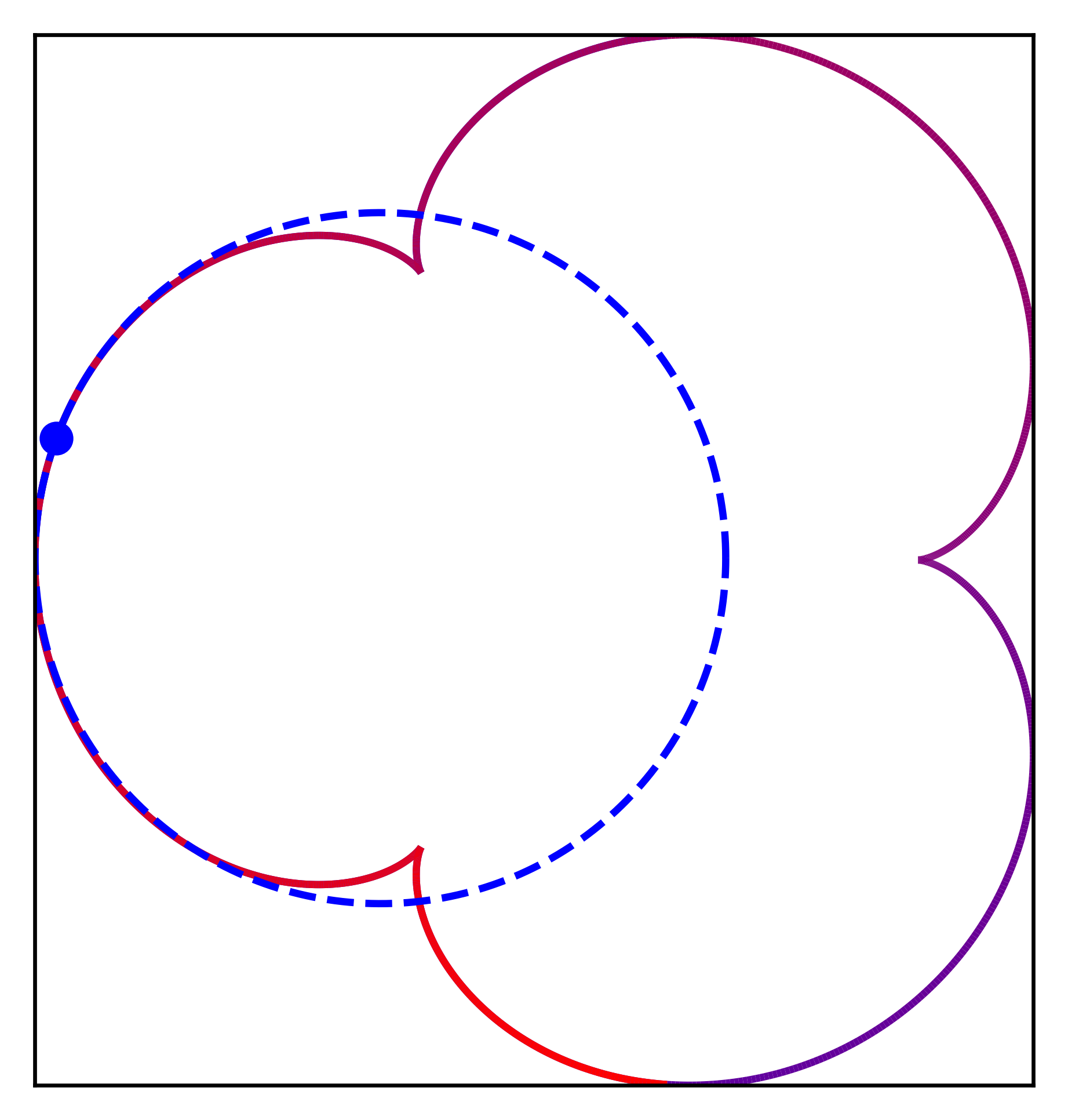
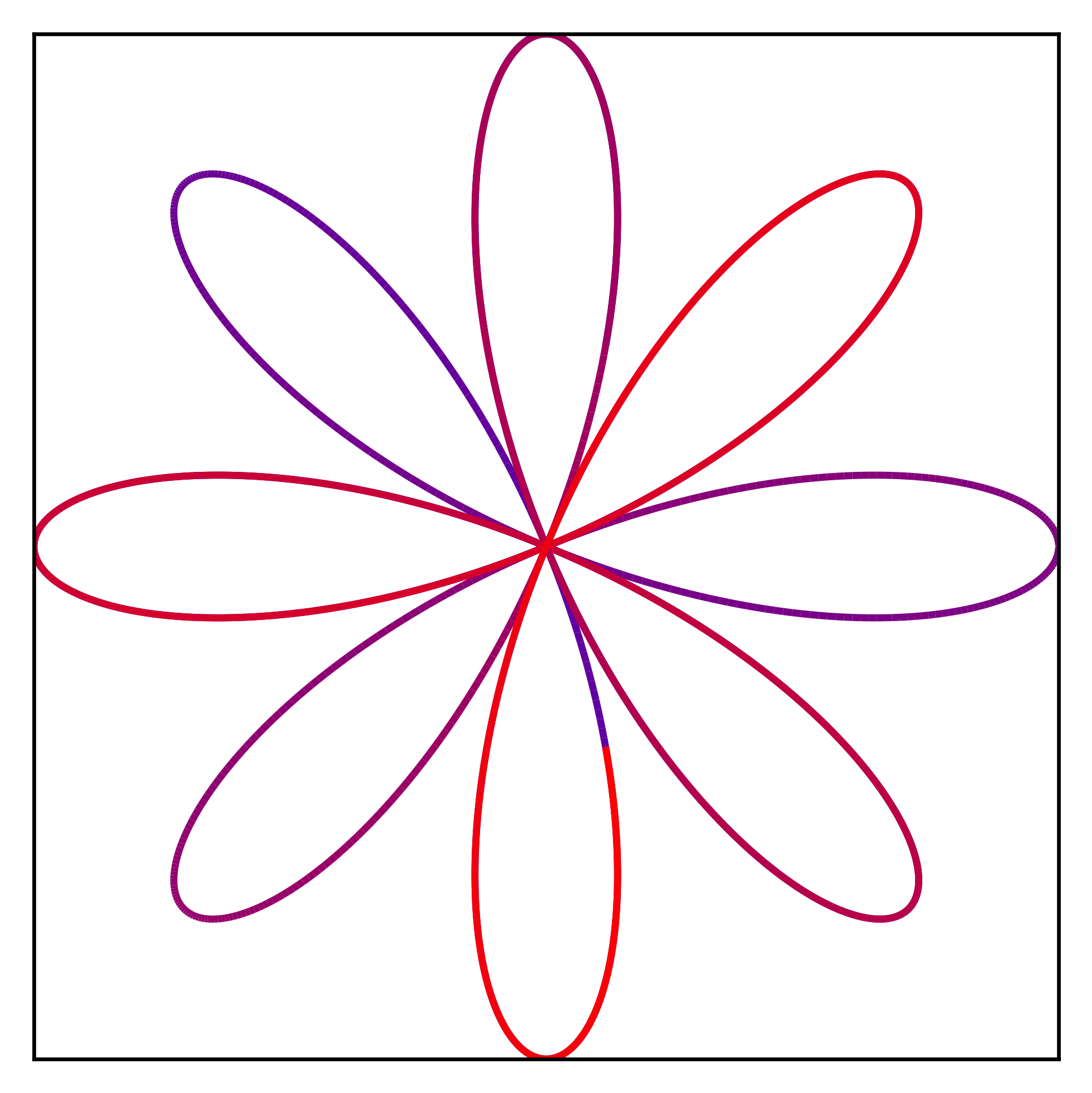
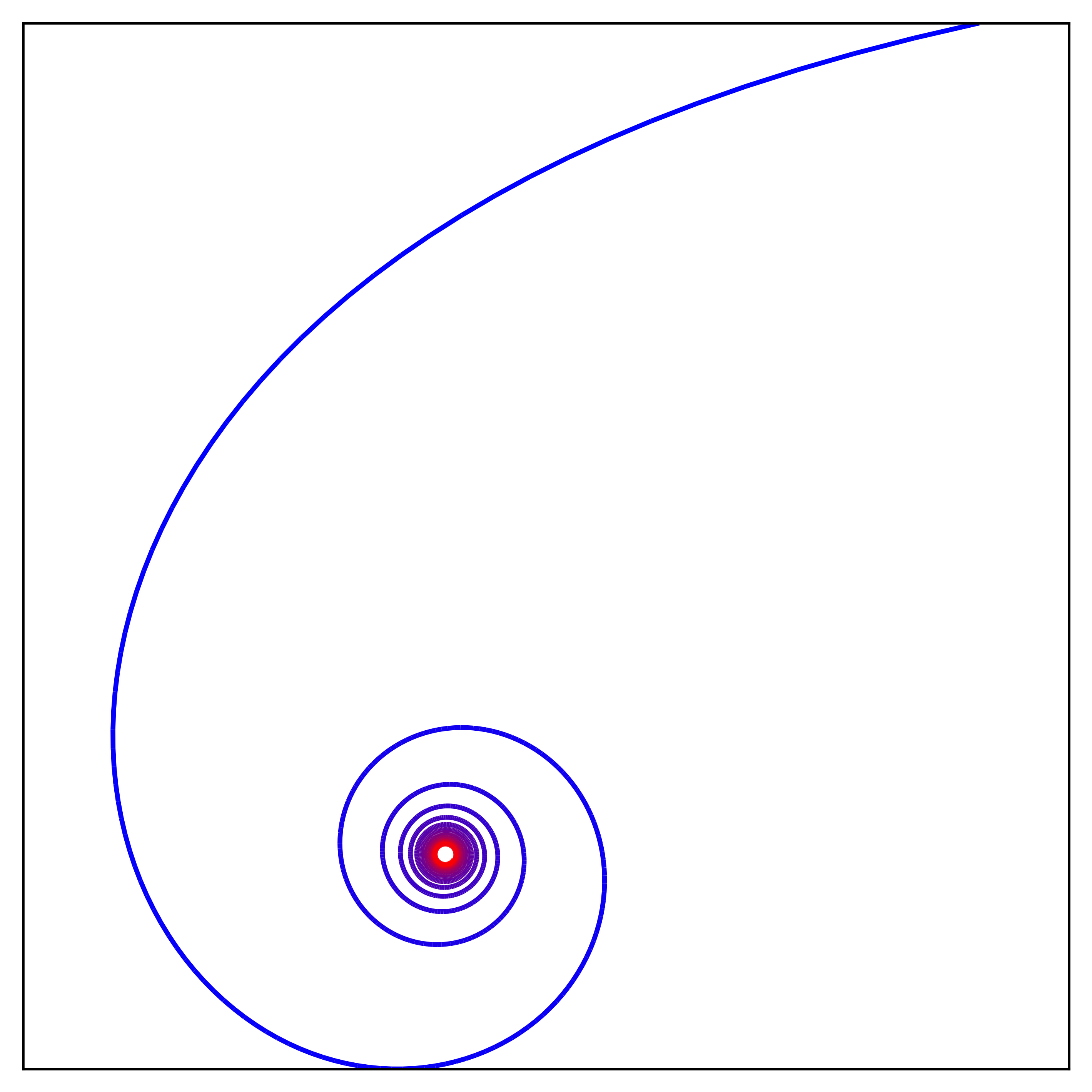
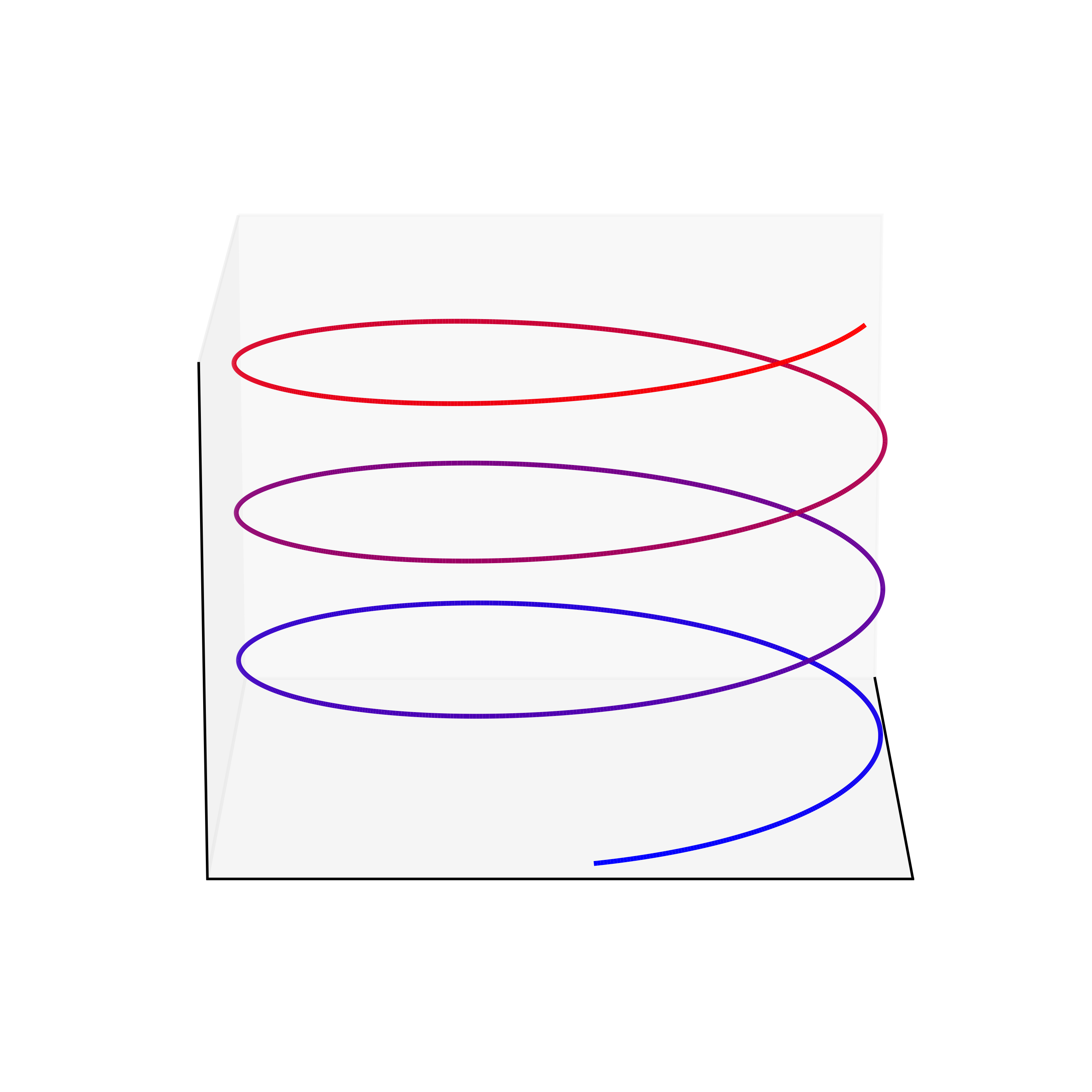
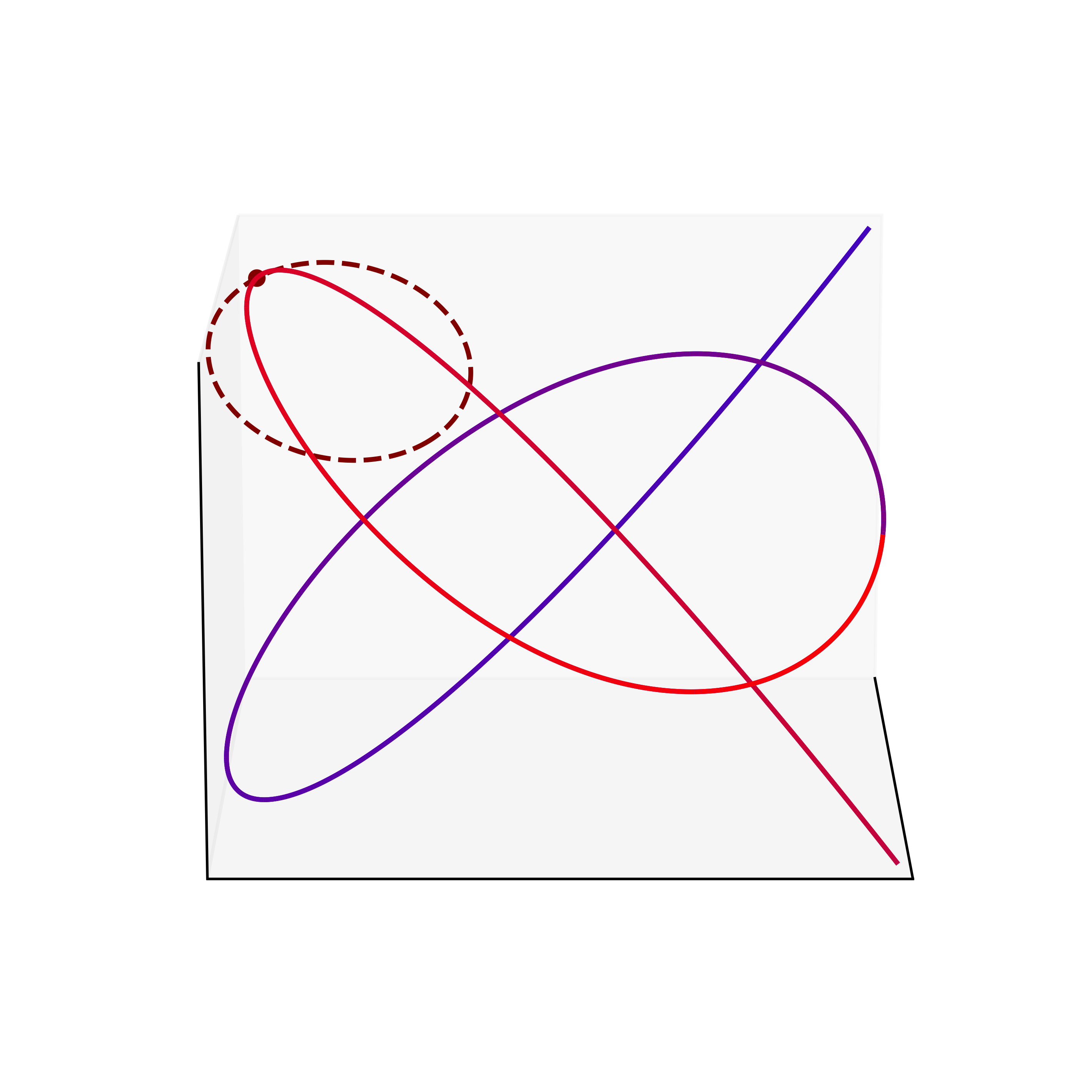
C'est juste un petit code Python qui demande en entrée la paramétrisation d'une courbe plane ou gauche (seulement avec des puisances, racines, exp, log et des fonctions trigos) et affiche son tracé. Il est aussi possible de faire apparaître le cercle ou le plan osculateur (quand c'est possible !). Voici des exemples :
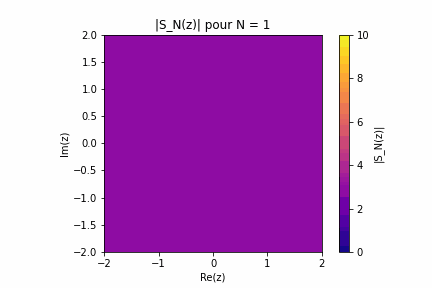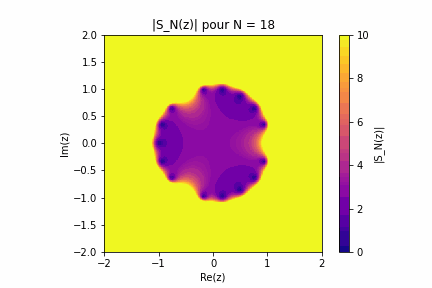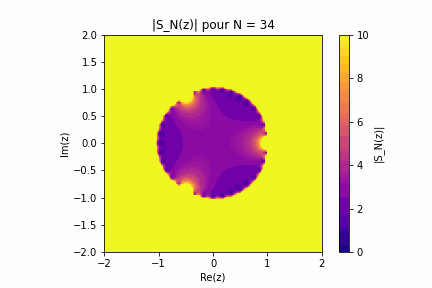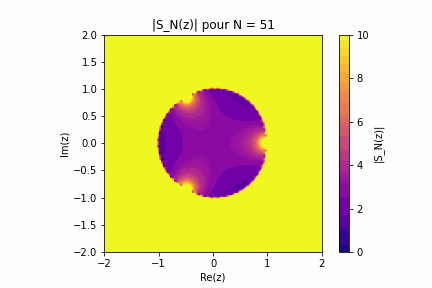
Un code python qui permet de visualiser la convergence d'une série entière dans le plan complexe. Il demande à l'utilisateur en entrée les coefficients \(a_n\) de la série \(S\) puis donne un gif de 50 images représentant la \(\vert S_N\vert\). L'execution est un peu longe, et le fichier gif se trouve dans le répertoire de travail. C'est pratique pour se faire une idée de la vitesse de convergence d'une série. A titre d'exemple, on trouvera ci-dessous l'animation pour une série qui converge sur le disque unité et explose en trois points du bord. Pour construire une telle série on peut s'inspirer de \(\sum^{\infty}_{n=0}z^n=\frac{1}{1-z}\) qui diverge en \(z=1\). On construit alors : \[ S(z) = \sum_{k=1}^3 \frac{c_k}{1 - z e^{-i\theta_k}} \] Or, comme pour \( |z| < 1 \), on a : \( \frac{1}{1 - z e^{-i\theta_k}} = \sum_{n=0}^\infty \left(z e^{-i\theta_k}\right)^n \) on est alors en droit d'écrire : \[ S(z) = \sum_{k=1}^3 c_k \sum_{n=0}^\infty \left(z e^{-i\theta_k}\right)^n \] Puis, par permutation des sommes (justifiée pour \( |z| < 1 \)), on obtient : \( S(z) = \sum_{n=0}^\infty \left( \sum_{k=1}^3 c_k e^{-i n \theta_k} \right) z^n \) On définit donc les coefficients : \[ a_n = \sum_{k=1}^3 c_k e^{-i n \theta_k} \] La série ainsi construite admet pour seuls points de divergence les \(e^{i\theta_k}\) En voici la représentation :
Enfin, voici une petite liste de sites qui valent le détour.